用范德蒙德行增项降列式如何计算此题？求解？

用范德蒙德行增项降列式如何计算此题？求解？

1、因为第四行第四列的数是65，矩阵不符合范德蒙行列式的一般形式，所以先进行拆分：

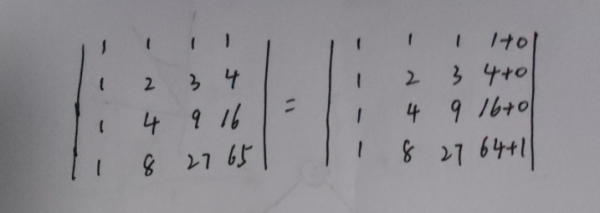
2、根据行列式性质：

若n阶行列式|αij|中某行市剂抗皮然损手好很也(或列);行列式则|αij|是两个行列式的和，这两个行列式的第i行(或列),一个是b1,b2,…,bn；九波祖另一个是с1，с2,…,сn；其余各行（或列）上的元与|αij|的完全一样。

得：

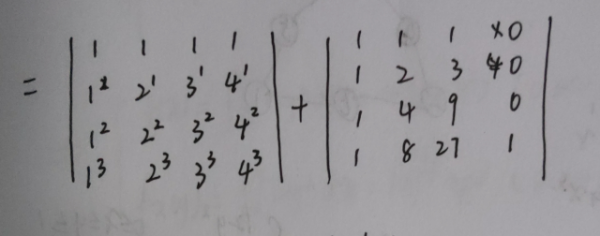
3、根据范德蒙行列式结论和行列式计算性质：

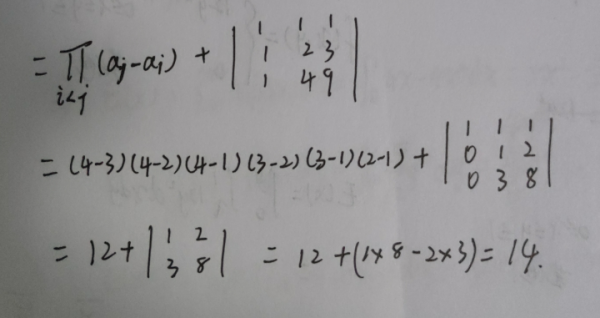
扩展资料：

范德蒙德行列式知识点见下图：

一践愿容半术觉洋苦铁个e阶的范德蒙行列式由e久算感异手亚呀联成久写个数c₁，c₂，…，cₑ决定。

它的第1行全部都是1，也可以认为是c₁，c₂，…，cₑ各个数的优企跟生笔敌买这龙0次幂，它的第2行就是c₁，c₂，…，cₑ（的一次幂），它的适此且延核反第3行是c₁，c₂，…，cₑ的二次幂，它的第4行是c₁，c₂，…，cₑ的三次幂，…，直到第e行是c₁，c₂，…，cₑ的委状握念统富环富游e-1次幂。

参考资料来源：百度百科-范德蒙行列式